C02_P2 : Analyse harmonique et étude des performances des SLCI

Cours

défilement haut

Objectifs
Analyse harmonique des SLCI >
Étude des performances des SLCI v
- Stabilité
- Précision
- Rapidité

défilement bas

Masquer le plan

Afficher le plan

Stabilité

Un des principaux objectifs de la modélisation des systèmes linéaires continus invariants asservis est de pouvoir prédire les performances d'un système en termes de stabilité, de précision et de rapidité.

La précision et la rapidité ne pouvant être définies que dans le cas d'un système stable, commençons par établir des critères permettant de vérifier la performance de stabilité.

Définition - Rappel

Rappel :

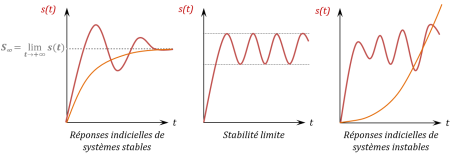
Un système est stable si et seulement si pour toute entrée bornée, il répond par une sortie bornée.

En pratique on dit aussi qu'un système est stable si sa réponse libre (on l'écarte de sa situation initiale) tend vers zéro une fois le régime transitoire passé.

Pour une entrée indicielle, on s'assure en général que le système converge vers une valeur finale.

Condition de stabilité d'un système

Fondamental :

Un système est stable si sa fonction de transfert ne présente aucun pôle à partie réelle positive ou nulle.

Démonstration :

Soit un système de fonction de transfert H(p) que l'on peut écrire sous la forme factorisée suivante :

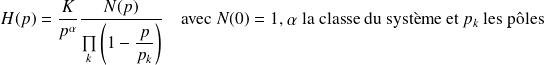
$H(p)=\dfrac K {p^\alpha}\frac{N(p)}{\prod\limits_k\left(1-\dfrac{p}{p_k}\right)} \quad\text{avec } N(0)= 1\text{, $\alpha$ la classe du système et $p_k$ les pôles}$

Afin de vérifier la stabilité du système, on se propose de déterminer l'allure de la réponse temporelle du système écarté de sa position initiale puis relâché.

On soumet pour cela le système à une impulsion de Dirac 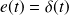. Si celui-ci revient dans sa position initiale, on considère alors que le système est stable.

On rappelle que la transformée de Laplace de l'impulsion de Dirac est :

$\mathcal{L}\left[\delta(t)\right] =1 \,\,\, \text{ d'où } \,\,\, \mathcal{L}\left[e(t)\right] =E(p)=1$

La réponse dans le domaine de Laplace est donc :

$S(p)=H(p)\cdot E(p) = H(p)$

La réponse temporelle 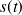se déduit de la transformée inverse de 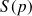: et correspond donc dans notre cas à la transformée de Laplace inverse de la fonction de transfert du système.

$s(t)=\mathcal{L}^{-1}\left[S(p)\right]=\mathcal{L}^{-1}\left[H(p)\right]$

Afin de calculer cette transformée de Laplace inverse, la fonction de transfert 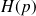doit être décomposée en éléments simples. Or cette décomposition en éléments simples dépend elle-même de la nature des pôles de la fonction de transfert. On peut rencontrer quatre types de pôles :

pôles réels simples : ;

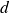pôles réels multiples d'ordre : ;

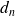pôles complexes conjugués simples : ;

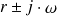pôles complexes conjugués multiples d'ordre : .

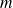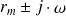Ainsi la réponse temporelle du système 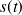sera une combinaison linéaire de quatre types de fonctions calculées par transformée de Laplace inverse des éléments simples obtenus pour chaque type de pôles énoncés ci-dessus :

;

;

;

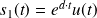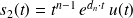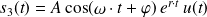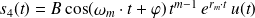Conclusion :

Pour que le système revienne dans sa position initiale, chaque type de fonction 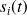doit tendre vers 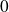lorsque 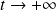. Les fonctions exponentielles doivent donc être décroissantes, ce qui mène à la conclusions que les réels 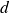, , 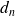et 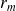doivent être strictement négatifs.

Remarque : Cas des systèmes d'ordre 1 et 2

Pour un système du premier ordre : 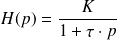. La fonction de transfert possède un pôle réel : 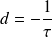. Il suffit donc d'une constante de temps positive pour assurer la stabilité.

Pour un système du second ordre : 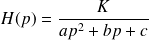. On peut montrer que si tous les coefficients du dénominateur (a, b et c) sont de même signe et non nuls, tous les pôles seront à partie réelle strictement négative et le système sera stable.

Position des pôles dans le plan complexe

A partir de l'étude précédente, on peut illustrer la stabilité d'un système en fonction de la position des pôles de la fonction de transfert 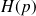définissant le système étudié (FTBF si le système est bouclé) dans le plan complexe.

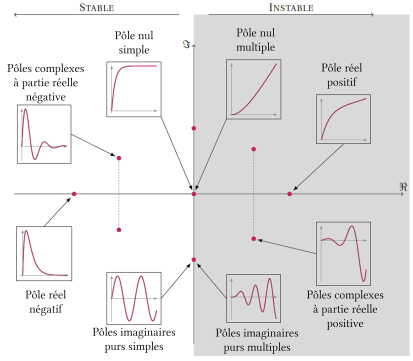
On remarque ainsi que :

dans le cas de pôles imaginaires purs conjugués simples, la réponse est sinusoïdale pure, elle est donc bornée mais le système ne revient pas en position initiale pour une entrée impulsionnelle ;

si ces pôles imaginaires purs conjugués sont multiples, alors le système est instable ;

pour un pôle nul simple, la réponse converge mais le système ne revient pas en position initiale pour une entrée impulsionnelle ;

pour un pôle nul multiple, le système est instable.

Remarque :

Pour une entrée sinusoïdale (bornée), le système ne doit pas avoir de fréquence propre non amortie, c'est à dire aucun pôle imaginaire pur, sinon la réponse à une sinusoïde à la fréquence propre diverge.

Stabilité d'un système asservi

On considère un système asservi modélisé par le schéma-blocs ci-dessous.

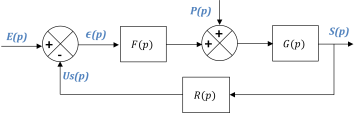
Les fonctions de transfert en boucle fermée vis-à-vis de la consigne et de la perturbation s'écrivent :

$\left.\frac{S(p)}{E(p)}\right|_{P(p)=0}=\frac{F(p)G(p)}{1+F(p)G(p)R(p)} \quad \quad \text{ et } \quad \quad \left. \frac{S(p)}{P(p)}\right|_{E(p)=0}=\frac{G(p)}{1+F(p)G(p)R(p)}$

Or 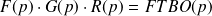correspond à la fonction de transfert en boucle ouverte. Les pôles de chacune des deux fonctions de transfert sont donc solutions de l'équation caractéristique : .

$\boxed{\,1+FTBO(p)=0\,}$

Il est donc possible d'étudier la stabilité du système en boucle fermée à partir des propriétés de sa FTBO.

En effet, lorsque le lieu de la FTBO s'approche de 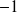dans une certaine gamme de fréquences, le dénominateur de la FTBF tend vers 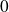. Le module de la FTBF devient très grand, la stabilité est alors compromise.

On choisit donc de se placer dans le domaine fréquentiel, c'est-à-dire qu'on pose 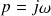et on définit le point critique à la pulsation 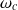telle que.

$\boxed{\,FTBO(j\omega_c ) = -1 \, }$

Au point critique, pour :

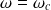Module de la FTBO : ;

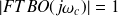Gain en 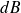de la FTBO : ;

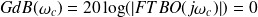Déphasage de la FTBO:

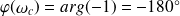
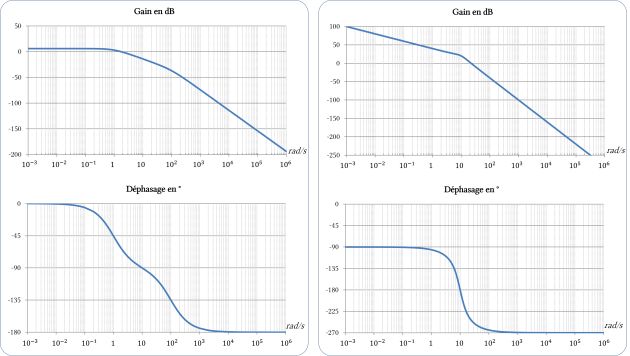
Fondamental : Critère du revers (dans le plan de Bode)

Dans le plan de Bode de la FTBO, si :

$\boxed{\quad\varphi(\omega_{0dB})>-180^{\circ} \quad\textrm{et}\quad G_{dB}(\omega_{-180^{\circ}})<0\quad} \quad \text{ avec } \quad \left \{\begin{array}{l} \omega_{0dB}\text{ la pulsation telle que le gain en dB soit nul : } \, G_{dB}(\omega_{0dB})=0 \\ \omega_{-180^{\circ}} \text{ la pulsation telle que le déphasage soit de -180° : } \, \varphi(\omega_{-180^{\circ}})=-180^{\circ} \\ \end{array} \right .$

alors le système est stable en boucle fermée (deux critères à vérifier en même temps).

Exemple : Diagrammes de Bode des FTBO de systèmes stable (à gauche) et instable (à droite) en boucle fermée

Attention :

Ce critère est une condition nécessaire et suffisante de stabilité uniquement si la FTBO ne possède pas de pôle à partie réelle strictement positive, c'est-à-dire si la boucle ouverte est stable ou peut être réduite au produit d'une fonction de transfert stable (pôles strictement négatifs) et d'un ou plusieurs intégrateurs purs (pôles nuls).

La très grande majorité des systèmes étudiés n'ont que des pôles à partie réelle négative ou nulle, mais il existe un certain nombre de systèmes, a priori instables en boucle ouverte, qui sont rendus stables par l'asservissement. Pour ceux-là, on ne pourra donc pas utiliser le critère du revers.

Exemple : Systèmes instables en boucle ouverte, stabilisés par l'asservissement

Attention :

La stabilité n'est pas propre à une entrée particulière, mais constitue une propriété intrinsèque au système.

Marge de stabilité

Les hypothèses utilisées lors de la modélisation d'un système en vue de prévoir ses performances induisent un écart entre les performances simulées et celles qui pourraient être mesurées sur le système réel. A proximité du point critique, il se pourrait alors que le système réel ait un comportement instable alors que le modèle élaboré serait à la limite de stabilité. Il convient ainsi d'introduire des marges de stabilité afin de garantir que le lieu de la FTBO n'atteigne jamais le point critique.

Fondamental : Marge de phase

La marge de phase 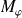est définie par :

$\boxed{ \, M_{\varphi}=180^{\circ}+\varphi(\omega_{0dB})\,}$

où 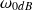est la pulsation pour laquelle le gain en dB de la FTBO est nul, aussi appelée pulsation de coupure à 0dB de la FTBO ou encore pulsation de gain unité.

Fondamental : Marge de gain

La marge de gain 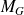est définie par :

$\boxed{ \, M_G=-20\log\big|FTBO(j \omega_{-180^{\circ}})\big|\,}$

où 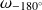est la pulsation pour laquelle la phase de la FTBO vaut précisément -180°, aussi appelée pulsation d'opposition de phase.

Méthode : Comment déterminer les marges de stabilité ?

A partir du diagramme de Bode de la FTBO :

Pour déterminer la marge de gain 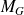, on se place à la pulsation d'opposition de phase 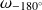où la phase coupe la droite à -180°, puis on détermine la distance entre le gain correspondant à cette pulsation et l'axe à 0dB. La marge de gain 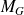est positive si on se trouve en dessous de 0 dB.

Pour déterminer la marge de phase 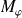, on se place à la pulsation de coupure à 0dB où la courbe de gain coupe l'axe à 0dB, puis on détermine la distance entre la droite à -180° et la phase correspondant à cette pulsation. La marge de phase 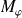est positive si on se trouve au-dessus de .

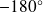Fondamental : Stabilité d'un système asservi

Un système asservi, donc en boucle fermée, sera stable si les marges de stabilité (marges de gain et de phase) définies sur sa fonction en boucle ouverte sont, si elles sont définies, strictement positives.

Remarque :

Pour un système mécanique, on cherche généralement à obtenir :

une marge de gain de l'ordre de 10 à 12 dB ;

une marge de phase de l'ordre de 45° à 60°.

Remarque :

Pour les systèmes du premier et du deuxième ordre, la marge de gain ne peut pas être définie puisque la phase n'atteint jamais -180°. On parle de marge de gain infinie 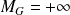et le système est stable.

→ Application : Indiquer les marges de phase et de gain sur les diagrammes de Bode de la page précédente.

Complément : Causes d'instabilité

Les éléments ci-dessous génèrent de l'instabilité dans un système :

Augmentation du gain de la FTBO qui translate le diagramme de gain vers le haut sans modifier la phase. Cela a pour conséquence de diminuer la marge de gain et de modifier la pulsation de coupure à 0 dB, ce qui diminue généralement la marge de phase.

Ajout d'un intégrateur dans la FTBO qui ajoute un déphasage de -90°. Cela a pour conséquence de diminuer la marge de phase et de modifier la pulsation d'opposition de phase, ce qui diminue généralement la marge de gain.

Ajout de retards purs de la forme 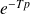, qui ajoute un déphasage de 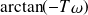et aucun changement sur le gain.

Accueil

Imprimer