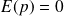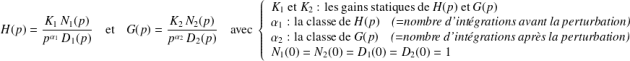Précision
Rappels
On considère un système asservi modélisé par le schéma-blocs suivant :
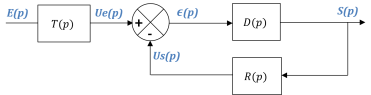
Rappel :
La précision qualifie l'aptitude du système à atteindre la valeur visée. Elle est caractérisée par l'erreur entre la consigne et la valeur effectivement atteinte par la grandeur de sortie en régime permanent, à condition que les grandeurs soient comparables (mêmes unités).
Rappel :
Le calcul de l'erreur nécessite que les grandeurs d'entrée
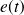 et de sortie
et de sortie
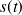 soient comparables. Si ce n'est pas le cas, on utilise plutôt l'écart
soient comparables. Si ce n'est pas le cas, on utilise plutôt l'écart
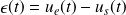 en sortie du comparateur en régime permanent.
en sortie du comparateur en régime permanent.
Cas d'étude
On considère désormais un système à deux entrées : consigne et perturbation, modélisé par le schéma-blocs suivant :
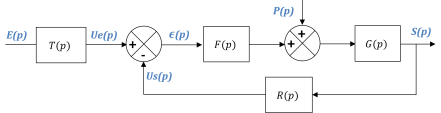

Afin que l'écart en sortie de comparateur soit l'image de l'erreur, on choisit un transducteur tel que
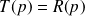 . On peut dans ce cas modéliser le système par le schéma-blocs à retour unitaire suivant :
. On peut dans ce cas modéliser le système par le schéma-blocs à retour unitaire suivant :

La réponse totale
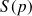 s’obtient en superposant la réponse
s’obtient en superposant la réponse
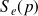 à une consigne
à une consigne
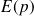 et la réponse
et la réponse
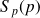 à une perturbation
à une perturbation
 :
:
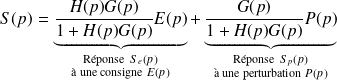
En remarquant que
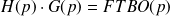 , on peut réécrire la réponse totale S(p) sous la forme suivante :
, on peut réécrire la réponse totale S(p) sous la forme suivante :
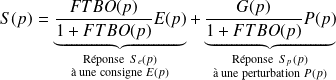
On rappelle qu'il existe deux modes de fonctionnement des systèmes asservis :
le mode suiveur, ou encore en poursuite, lorsque la sortie suit la consigne en l'absence de perturbations ;
le mode régulateur, ou en régulation, lorsque la sortie suit une consigne constante (généralement nulle) tout en rejetant les perturbations.
La précision d'un système se détermine séparément en poursuite et en régulation.
Précision en poursuite
La précision en poursuite est déterminée en supposant que la perturbation soit nulle :
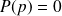 .
.
L'erreur en poursuite est donnée par :
On pose alors :
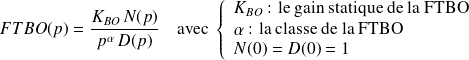
Ainsi :
Enfin, d'après le théorème de la valeur finale :
Fondamental :
L'erreur en poursuite d'un système est donnée par :

Le tableau suivant donne l'erreur statique et l'erreur de traînage en fonction de la classe de la FTBO :

Conclusion :
La présence d'intégrateurs dans la FTBO peut annuler l'erreur, et améliore donc la précision. La précision est donc directement liée à la classe de la FTBO.

Précision en régulation

Fondamental :
Pour une perturbation de la forme
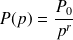 :
:
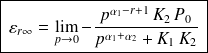
Trois cas sont alors à distinguer :
si
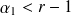 , alors
, alors
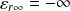 ;
;
si
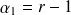 , alors
, alors
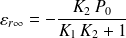 si
si
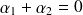 ou
ou
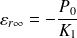 si
si
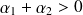 ;
;
si
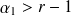 , alors
, alors
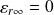 .
.
Conclusions :
Seules les intégrations en amont de la perturbation ont une influence sur la précision, elles peuvent annuler l'erreur en fonction de la nature de la perturbation.
En particulier, pour une perturbation en échelon, un seul intégrateur en amont de la perturbation est suffisant pour annuler l'erreur. Ce point sera particulièrement pris en compte dans le choix du correcteur, objet du programme de deuxième année.
Un système qui est précis en régulation est dit robuste.
Précision dans le cas général
Pour un système à deux entrées (consigne et perturbation), l'erreur dans le cas général
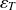 s'obtient en superposant l'erreur de poursuite
s'obtient en superposant l'erreur de poursuite
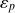 et l'erreur de régulation
et l'erreur de régulation
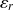 :
:
Remarque : Généralisation pour un système à n entrées
Pour un système à
 entrées, l'erreur se détermine alors en superposant les erreurs obtenues vis-à-vis de chacune des
entrées, l'erreur se détermine alors en superposant les erreurs obtenues vis-à-vis de chacune des
 entrées.
entrées.