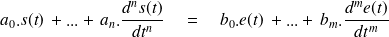Présentation
Soit un système linéaire continu et invariant d'entrée
|  |
Lors d'une étude harmonique, le système est sollicité par une entrée sinusoïdale du type :
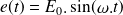. Le principe de l'étude fréquentielle repose sur le constat suivant :
Fondamental :
Tout système dynamique régi par une équation différentielle d'ordre n à coefficients constants soumis à une excitation d'entrée
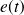de type sinusoïdale, donne une réponse
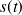en régime établi qui est de forme sinusoïdale, de même fréquence que l'entrée mais d'amplitude différente et déphasée.
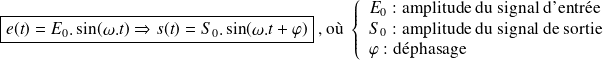
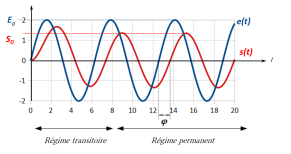
Dans une étude harmonique, on se place en régime permanent, lorsque
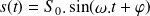. La pulsation
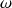est imposée par le signal d'entrée. Il suffit donc de déterminer
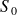(ou le gain
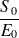) et
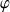pour connaître la réponse harmonique du système.
